Jawab:
Persamaan van der Waals merupakan persamaan modifikasi dari gas ideal yang cocok untuk perhitungan gaya tarik menarik antara partikel gas akibat pengaruh tekanan. Semakin besar molekul partikel akan menurunkan temperatur kritis.
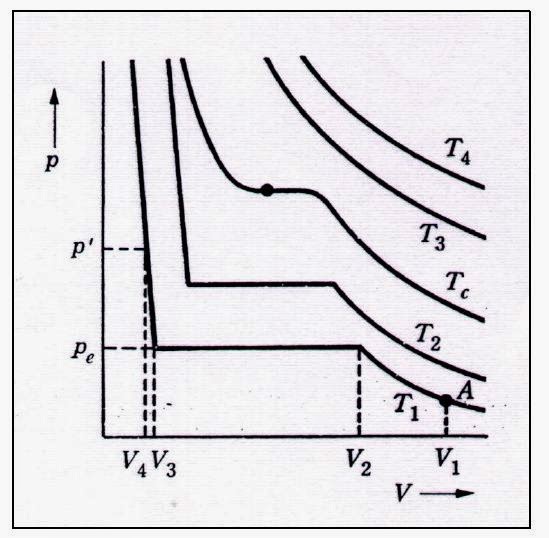
Pada titik kritis, nilai perubahan tekanan akibat perubahan volume pada temperatur kritis akan bernilai sama dengan nol. Hal ini dapat dijelaskan pada diagram P-V untuk temperatur kritis sebagai berikut.
Dari grafik diatas dapat dijelaskan beberapa hal berikut :
1. Pada T1 dan V1, ketika volume gas turun, tekanan meningkat.
2. Dari V2 ke V3, tidak ada perubahan tekanan meskipun volume turun.
3. Tekanan meningkat tinggi setelah V3
4. Pada temperatur diatas T2, daerah plato (liquid+vapor) menjadi lebih pendek.
5. Tc merupakan temperatur kritis, volume dan tekanan pada titik itu adalah volume dan tekanan kritis.
6. Ketika T > Tc gas uncompressible menjadi fluida. Pada titik temperatur kritis, (T = constant) dalam P-V diagram akan memiliki 2 titik balik dimana turunan-1 dan turunan-2 dari perubahan tekanan akibat volume pada kondisi isothermal = 0. Hal ini dapat terlihat pada grafik dibawah ini.
Dengan menggunakan pendekatan sifat pada daerah kritis pada kondisi isotermal, dapat ditentukan nilai a dan b dari persamaan umum van der Waals, dimana
Substitusi nilai volume kritis Vc and temperatur kritis Tc kedalam persamaan Van der Waals memberikan
Karena fungsi a dan b yang akan dicari merupakan fungsi dari titik kritis (temperatur dan tekanan kritis), maka
Nilai b tersebut di substitusi kedalam persamaan Tc untuk menghasilkan nilai a, menghasilkan
Terbukti








No comments:
Post a Comment